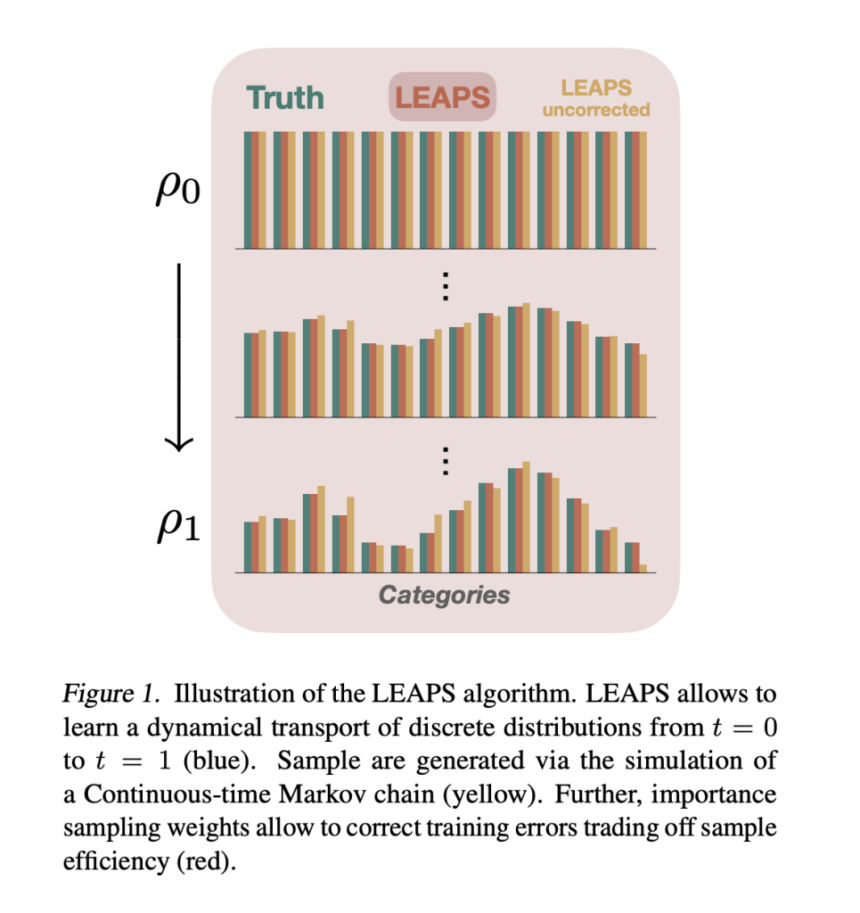
Sampling from probability distributions with known density functions (up to normalization) is a fundamental challenge across various scientific domains. From Bayesian uncertainty quantification to molecular dynamics and quantum physics, the ability to efficiently generate representative samples is crucial. While Markov chain Monte Carlo (MCMC) methods have long been the dominant approach, they often suffer from slow convergence, especially when dealing with multimodal distributions.
Traditional MCMC methods frequently struggle with convergence to equilibrium, leading researchers to combine them with non-equilibrium dynamics through techniques like annealed importance sampling (AIS) or sequential Monte Carlo (SMC). However, these methods can still exhibit high variance in their importance weights, resulting in inefficient sampling. The integration of deep learning with sampling algorithms has shown promise in continuous domains, but there remains a significant gap in effective sampling approaches for discrete distributions – despite their prevalence in applications ranging from statistical physics to genomic data and language modeling.
The research team addresses this gap with LEAPS (Locally Equivariant discrete Annealed Proactive Sampler), a novel sampling method that leverages continuous-time Markov chains (CTMCs) to efficiently sample from discrete distributions. LEAPS combines the theoretical foundation of non-equilibrium dynamics with neural network-based learning to create a powerful sampling approach.
LEAPS works by constructing a time-dependent probability path (ρt) that begins with an easy-to-sample distribution (ρ0) and gradually transforms it into the target distribution (ρ1). The central innovation lies in designing a CTMC whose evolution follows this prescribed path, enabling efficient sampling through a combination of:
- Proactive Importance Sampling: The researchers developed a novel importance sampling scheme that anticipates where the CTMC will jump next, accumulating weights that reflect the deviation from the true distribution.
- Locally Equivariant Neural Networks: A key computational breakthrough that allows efficient calculation of importance weights without the prohibitive costs associated with evaluating all neighboring states.
- PINN Objective: A physics-informed neural network objective that trains the CTMC rate matrix by minimizing the variance of importance sampling weights.
Traditional approaches would require evaluating the neural network for each neighbor of a state, making the computation of importance weights prohibitively expensive for high-dimensional spaces. LEAPS introduces the concept of “local equivariance” – an inductive bias that enables computing these weights in a single forward pass of the neural network.
A locally equivariant neural network ensures that the “flux of probability” from a state to its neighbor is exactly negative of the flux from the neighbor back to the state. This property allows the model to efficiently capture the dynamics of the system without redundant calculations.
The research team demonstrates how to construct locally equivariant versions of popular neural network architectures:
- Multilayer Perceptrons (MLPs) with specifically constrained weight matrices
- Locally-Equivariant Attention (LEA) layers that maintain the equivariance property
- Locally-Equivariant Convolutional (LEC) networks that can be stacked into deep architectures
LEAPS is not just computationally efficient but also theoretically sound. The researchers prove that their proactive importance sampling scheme provides unbiased estimates and that the locally equivariant parameterization of rate matrices is universally expressive – meaning it can represent any valid CTMC for the sampling problem.
A noteworthy theoretical result is that LEAPS generalizes both AIS and SMC methods. When the neural network component is set to zero, LEAPS recovers these classical approaches, making it a strict superset of these well-established sampling techniques.
To demonstrate LEAPS in action, the researchers applied it to sampling from a 2D Ising model – a classic challenge in statistical physics. Working with a 15×15 lattice (a 225-dimensional discrete space), they compared different neural architectures implementing their method against ground truth samples generated by long-run Glauber dynamics.
The results are impressive:
- Convolutional architectures outperformed attention-based models, with deeper networks yielding better results
- LEAPS accurately captured the magnetization distribution and two-point correlation functions
- The method achieved high effective sample size (ESS), indicating efficient sampling with low-variance importance weights
- LEAPS significantly outperformed pure MCMC approaches with the same number of sampling steps
What makes LEAPS particularly valuable is its ability to handle high-dimensional discrete spaces, which are ubiquitous in real-world applications but notoriously challenging for sampling algorithms. The method combines the statistical guarantees of traditional approaches with the representational power of deep learning. Additionally, LEAPS can be integrated with existing MCMC schemes, effectively combining learned transport with traditional random walks to achieve better mixing properties. This hybrid approach provides a practical pathway for researchers to enhance their existing sampling methods.
In conclusion, LEAPS represents a significant advancement in sampling from discrete distributions, especially in high-dimensional settings. By leveraging locally equivariant neural networks and proactive importance sampling, it offers a computationally efficient approach with strong theoretical guarantees. The research team suggests several promising directions for future work, including extending LEAPS to sample from entire families of distributions simultaneously and applying the locally equivariant neural network architecture to other probabilistic modeling tasks. The connection between LEAPS and guidance or reward fine-tuning of generative CTMC models also presents an exciting avenue for further exploration.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, feel free to follow us on Twitter and don’t forget to join our 80k+ ML SubReddit.
The post LEAPS: A Neural Sampling Algorithm for Discrete Distributions via Continuous-Time Markov Chains (‘Discrete Diffusion’) appeared first on MarkTechPost.