Diffusion models are promising in long-horizon planning by generating complex trajectories through iterative denoising. However, their ability to improve performance through more computation at test time is minimal. In comparison to Monte Carlo Tree Search, whose strength lies in taking advantage of additional computational resources, typical diffusion-based planners will likely suffer from diminishing returns in the number of denoising steps or in producing additional trajectories. In addition, these models have difficulty with efficient exploration-exploitation trade-offs, leading to suboptimal performance in complex environments. Traditional Monte Carlo Tree Search methods, while giving good iterative improvement, suffer from high computational complexity in large, continuous action spaces. The biggest challenge is constructing a planning paradigm that takes advantage of the generative flexibility of diffusion models while combining the structured search benefit of Monte Carlo Tree Search, thereby enabling efficient and scalable decision-making in long-horizon problems.
State-of-the-art diffusion-based planners, such as Diffuser, generate complete trajectories in a holistic way, from which forward dynamics models are avoided. Even though this approach increases the consistency of trajectories, it lacks structured search methods, thus not suitable for enhancing suboptimal plans. Other methods, such as Diffuser-Random Search and Monte Carlo Guidance, attempt to utilize iterative sampling; however, they fail to systematically discard unpromising trajectories. Monte Carlo Tree Search, in contrast, leverages more computational resources, but its reliance on a forward model renders it unsuitable for extensive, continuous action spaces. These limitations create a wide gap in scalable and flexible planning, especially in domains with long-horizon trajectory optimization.
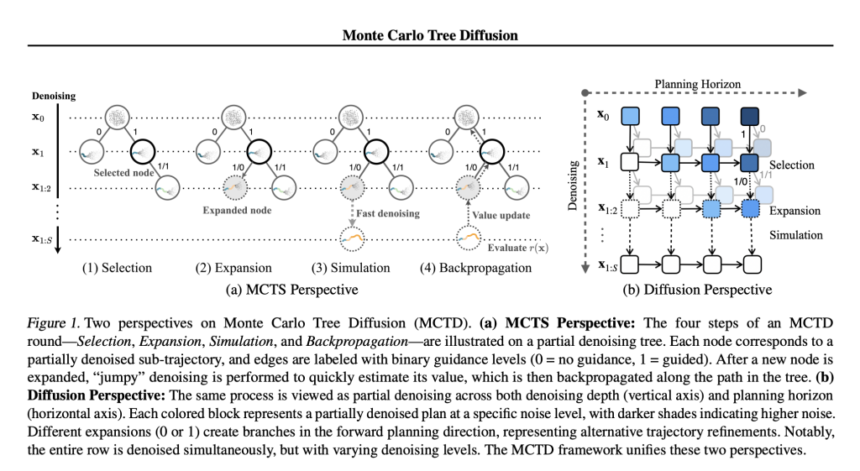
To compensate for these shortcomings, Monte Carlo Tree Diffusion combines tree search with diffusion-based planning, basically combining the systematic search of Monte Carlo Tree Search with the generative power of diffusion models. Instead of treating the denoising process as a standalone procedure, the approach reimagines it in a tree-structured rollout framework, thereby allowing for iterative evaluation, pruning, and refinement of partially denoised plans. The framework introduces three key innovations. First, the denoising process is reimagined as a tree-based expansion mechanism that allows for structured searching while maintaining trajectory coherence. Second, it applies adaptive exploration-exploitation trade-offs through guidance schedules, which adaptively adjust the refinement of trajectories. Third, instead of using full rollouts, a fast and approximated denoising method is used to rapidly evaluate trajectory quality, thereby reducing computational overhead. These improvements provide a scalable and flexible planning mechanism that promises to improve test-time performance as computational resources are increased.
Monte Carlo Tree Diffusion follows the four phases of Monte Carlo Tree Search—Selection, Expansion, Simulation, and Backpropagation—within the diffusion framework. The selection phase chooses the optimal subplans according to the Upper Confidence Bound criterion. The expansion phase generates new subplans with the diffusion model, with every step dynamically balancing exploration through random sampling and exploitation through goal-guided refinement. Simulation is done with efficient jumpy denoising algorithms to evaluate the quality of trajectories at little computational cost. Backpropagation then backpropagates the reward signal from the evaluated trajectories back through the tree, thus updating node values and dynamically adjusting the guidance schedule. The efficiency of this framework is evaluated using the OGBench, an offline goal-conditioned reinforcement learning benchmark involving tasks like maze navigation, robotic cube manipulation, and image-based planning. The planning horizons are chosen between 500 and 1000 steps, which allows a comprehensive comparison of its efficiency with baseline models like Diffuser, Diffuser-Replanning, and Diffusion Forcing.
Monte Carlo Tree Diffusion demonstrates state-of-the-art performance on a range of planning tasks, outperforming across-the-board diffusion-based and search-based baselines. On long-horizon maze navigation, it shows near-perfect success rates, far surpassing Diffuser and random search-based approaches, which do not scale. On robotic cube manipulation, it manages multi-object interactions well, preventing trajectory entanglements that make single-pass planners suffer. For image-based navigation under partial observability, it preserves high success rates, showing its capacity to balance exploration and exploitation even without direct state knowledge. Most notably, this approach scales well with extra test-time computation, constantly refining plans as standard diffusion techniques plateau, illustrating its power in structured search in generative models.
The combination of structured search and generative trajectory planning enabled by Monte Carlo Tree Diffusion enables scalable and high-quality decision-making in long-time-frame problems. Tree-based denoising, adaptive guidance schedules, and speeded-up simulation are significantly better than diffusion-based planners. Its ability to scale easily with more computational resources makes it a viable candidate for use in robotics, autonomous decision-making, and strategic planning. Improvements in adaptive compute allocation, meta-learning for better search, and self-supervised reward shaping can make it more scalable and applicable to more complex environments.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, feel free to follow us on Twitter and don’t forget to join our 80k+ ML SubReddit.
The post Monte Carlo Tree Diffusion: A Scalable AI Framework for Long-Horizon Planning appeared first on MarkTechPost.