Neural Ordinary Differential Equations are significant in scientific modeling and time-series analysis where data changes every other moment. This neural network-inspired framework models continuous-time dynamics with a continuous transformation layer governed by differential equations, which sets them apart from vanilla neural nets. While Neural ODEs have cracked down on handling dynamic series efficiently, cost-effective gradient calculation for backpropagation is a big challenge that limits its utility.
Until now, the standard method for N-ODEs has been recursive checkpointing that finds a middle ground between memory usage and computation. However, this method often presents inefficiencies, leading to an increase in both memory and processing time. This article discusses the latest research that tackles this problem through a class of algebraically reversible ODE solvers.
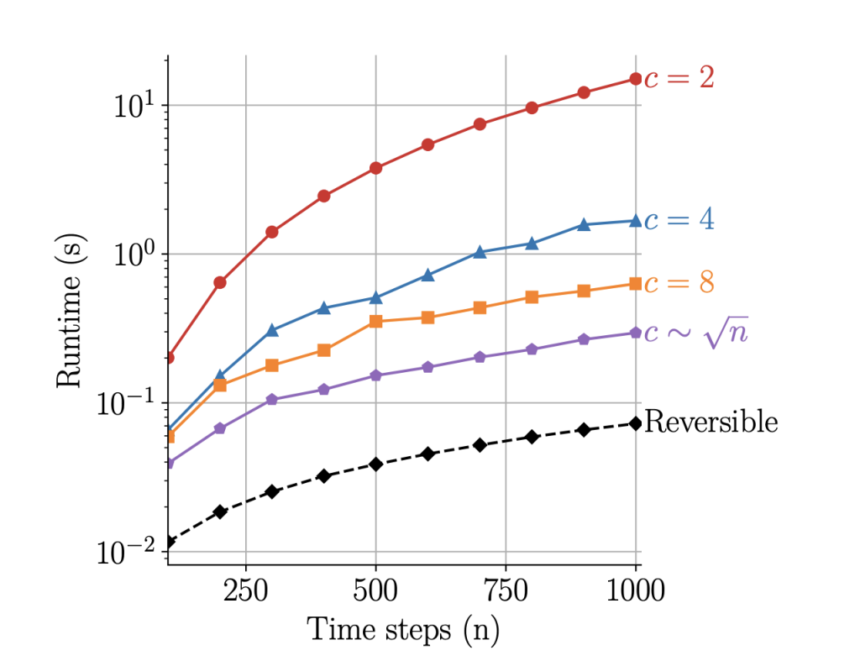
Researchers from the University of Bath introduce a novel machine learning framework to address the problem of backpropagation in the State-of-the-art recursive checkpoint methods in Neural ODE solvers. The authors introduce a class of algebraically reversible solvers that allows for the exact reconstruction of the solver state at any time step without storing intermediate numerical operations. These innovations lead to a significant improvement in the overall efficiency of the process with reduced memory consumption and computational overhead. The contrasting feature of this research that outshines this approach is its space complexity. While conventional solvers operate O(n log n), the proposed solver has O(n) complexity for operation and O(1) memory consumption.
The proposed solver framework allows any single-step numerical solver to be made reversible by enabling dynamic recomputation of the forward solve during backpropagation. This approach, therefore, ensures exact gradient calculation while achieving high-order convergence and improved numerical stability. The method’s working is further detailed: Instead of storing every intermediate state during the forward pass, the algorithm mathematically reconstructs these in reverse order during the backward pass. Furthermore, by introducing a coupling parameter, λ, the solver maintains numerical stability while accurately tracing the computational path backward. This coupling ensures that information from both the current and previous states is retained in a compact form, enabling exact gradient calculation without the overhead of traditional storage requirements.
The research team conducted a series of experiments to validate the claims of these solvers. They performed three experiments focussing on scientific modeling and latent dynamics discovery from the data to compare the accuracy, runtime, and memory cost of reversible solvers to recursive checkpointing. The solvers were tested against the following three experimental setups:
- Discovery of Generated data from Chandrasekhar’s White Dwarf Equation
- Approximation of fundamental data dynamics from a coupled oscillator system through a neural ODE.
- Identification of chaotic nonlinear dynamics using a chaotic double pendulum dataset
The results of the above experiments testified to the proposed solvers’ efficiency. Across all tests, these demonstrated superior performance, achieving up to 2.9 times faster training speeds and using up to 22 times less memory than traditional methods.
Moreover, the accuracy of the final model remained consistent when compared to the state of the art. The reversible solvers reduced memory usage dramatically and slashed runtime, proving its utility in large-scale, data-intensive applications. The authors also found that adding weight decay to the neural network vector field parameters improved numerical stability for both the reversible method and recursive checkpointing.
Conclusion: The paper introduced a new class of algebraic solvers that solves the issues of computational efficiency and gradient accuracy. The proposed framework has an operation complexity of O(n) and memory usage of O(1). This breakthrough in ODE solvers paves the way for more scalable and robust time series and dynamic data models.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. Don’t Forget to join our 75k+ ML SubReddit.
The post University of Bath Researchers Developed an Efficient and Stable Machine Learning Training Method for Neural ODEs with O(1) Memory Footprint appeared first on MarkTechPost.